Note
Click here to download the full example code
Use of Multi-Fidelity Kriging¶
from smt.applications import MFK,NestedLHS
import numpy as np
import otsmt
import matplotlib.pyplot as plt
import openturns as ot
Definition of Initial data
# Construction of the DOE
# low fidelity model
def lf_function(x):
return (
0.5 * ((x * 6 - 2) ** 2) * np.sin((x * 6 - 2) * 2)
+ (x - 0.5) * 10.0
- 5
)
# high fidelity model
def hf_function(x):
return ((x * 6 - 2) ** 2) * np.sin((x * 6 - 2) * 2)
# Problem set up
xlimits = np.array([[0.0, 1.0]])
xdoes = NestedLHS(nlevel=2, xlimits=xlimits, random_state=0)
xt_c, xt_e = xdoes(4)
# Evaluate the HF and LF functions
yt_e = hf_function(xt_e)
yt_c = lf_function(xt_c)
xv_e = np.linspace(xlimits[0][0],xlimits[0][1],50)[:,np.newaxis]
yv_e = hf_function(xv_e)
Out:
/usr/share/miniconda3/envs/test/lib/python3.9/site-packages/numpy/lib/function_base.py:2845: RuntimeWarning: Degrees of freedom <= 0 for slice
c = cov(x, y, rowvar, dtype=dtype)
/usr/share/miniconda3/envs/test/lib/python3.9/site-packages/numpy/lib/function_base.py:2704: RuntimeWarning: divide by zero encountered in divide
c *= np.true_divide(1, fact)
/usr/share/miniconda3/envs/test/lib/python3.9/site-packages/numpy/lib/function_base.py:2704: RuntimeWarning: invalid value encountered in multiply
c *= np.true_divide(1, fact)
Training of smt model for Multi-Fidelity Kriging
sm_mfk = MFK(theta0=xt_e.shape[1] * [1.0])
# low-fidelity dataset names being integers from 0 to level-1
sm_mfk.set_training_values(xt_c, yt_c, name=0)
# high-fidelity dataset without name
sm_mfk.set_training_values(xt_e, yt_e)
# train the model
sm_mfk.train()
Out:
___________________________________________________________________________
MFK
___________________________________________________________________________
Problem size
# training points. : 4
___________________________________________________________________________
Training
Training ...
Training - done. Time (sec): 0.0519252
Creation of OpenTurns PythonFunction for prediction
otmfk = otsmt.smt2ot(sm_mfk)
otmfkprediction = otmfk.getPredictionFunction()
otmfkpvariances = otmfk.getConditionalVarianceFunction()
otmfkgradient = otmfk.getPredictionDerivativesFunction()
print('Predicted values by MFK:',otmfkprediction(xv_e))
print('Predicted variances values by MFK:',otmfkpvariances(xv_e))
print('Prediction derivatives by MFK:',otmfkgradient(xv_e))
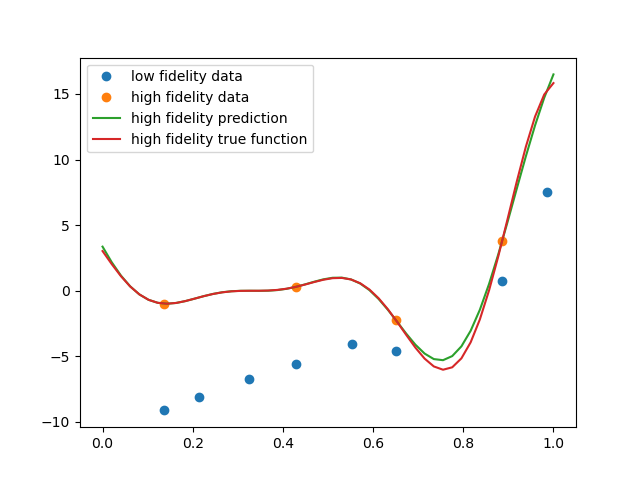
plt.figure()
plt.plot(xt_c,yt_c,'o',label='low fidelity data')
plt.plot(xt_e,yt_e,'o',label='high fidelity data')
plt.plot(xv_e,otmfkprediction(xv_e),label='high fidelity prediction')
plt.plot(xv_e,yv_e,label='high fidelity true function')
plt.legend()
Out:
___________________________________________________________________________
Evaluation
# eval points. : 50
Predicting ...
Predicting - done. Time (sec): 0.0003684
Prediction time/pt. (sec) : 0.0000074
Predicted values by MFK: [ y0 ]
0 : [ 3.36259 ]
1 : [ 2.17245 ]
2 : [ 1.15711 ]
3 : [ 0.33716 ]
4 : [ -0.278041 ]
5 : [ -0.691552 ]
6 : [ -0.918828 ]
7 : [ -0.986409 ]
8 : [ -0.929369 ]
9 : [ -0.787746 ]
10 : [ -0.602325 ]
11 : [ -0.410289 ]
12 : [ -0.241288 ]
13 : [ -0.114471 ]
14 : [ -0.0369421 ]
15 : [ -0.00389078 ]
16 : [ -0.000468516 ]
17 : [ -0.00519364 ]
18 : [ 0.00554832 ]
19 : [ 0.0525371 ]
20 : [ 0.149013 ]
21 : [ 0.296968 ]
22 : [ 0.485052 ]
23 : [ 0.68852 ]
24 : [ 0.871351 ]
25 : [ 0.990384 ]
26 : [ 1.001 ]
27 : [ 0.863646 ]
28 : [ 0.550373 ]
29 : [ 0.0504842 ]
30 : [ -0.62548 ]
31 : [ -1.44402 ]
32 : [ -2.34954 ]
33 : [ -3.2678 ]
34 : [ -4.1116 ]
35 : [ -4.78823 ]
36 : [ -5.20775 ]
37 : [ -5.29133 ]
38 : [ -4.97881 ]
39 : [ -4.23458 ]
40 : [ -3.05145 ]
41 : [ -1.45195 ]
42 : [ 0.51281 ]
43 : [ 2.7666 ]
44 : [ 5.2135 ]
45 : [ 7.74458 ]
46 : [ 10.2454 ]
47 : [ 12.6034 ]
48 : [ 14.715 ]
49 : [ 16.4913 ]
Predicted variances values by MFK: [ y0 ]
0 : [ 10.179 ]
1 : [ 5.4472 ]
2 : [ 2.59355 ]
3 : [ 1.05755 ]
4 : [ 0.344588 ]
5 : [ 0.0767776 ]
6 : [ 0.0067112 ]
7 : [ 0.000419647 ]
8 : [ 0.00301542 ]
9 : [ 0.00213815 ]
10 : [ 0.000283986 ]
11 : [ 0.000237495 ]
12 : [ 0.00148185 ]
13 : [ 0.00216881 ]
14 : [ 0.00155617 ]
15 : [ 0.000452678 ]
16 : [ 1.84457e-06 ]
17 : [ 0.000446884 ]
18 : [ 0.00105183 ]
19 : [ 0.00102818 ]
20 : [ 0.000409195 ]
21 : [ 2.54515e-07 ]
22 : [ 0.000496539 ]
23 : [ 0.00167399 ]
24 : [ 0.00249858 ]
25 : [ 0.00212468 ]
26 : [ 0.000850067 ]
27 : [ 7.85821e-06 ]
28 : [ 0.000686052 ]
29 : [ 0.00237432 ]
30 : [ 0.00307325 ]
31 : [ 0.00147847 ]
32 : [ 4.55678e-05 ]
33 : [ 0.00638104 ]
34 : [ 0.0307624 ]
35 : [ 0.0798767 ]
36 : [ 0.149854 ]
37 : [ 0.223325 ]
38 : [ 0.274021 ]
39 : [ 0.278435 ]
40 : [ 0.229328 ]
41 : [ 0.143252 ]
42 : [ 0.0559062 ]
43 : [ 0.00506563 ]
44 : [ 0.00840297 ]
45 : [ 0.0489685 ]
46 : [ 0.0809975 ]
47 : [ 0.0621786 ]
48 : [ 0.00761714 ]
49 : [ 0.0498522 ]
___________________________________________________________________________
Evaluation
# eval points. : 50
Predicting ...
Predicting - done. Time (sec): 0.0003324
Prediction time/pt. (sec) : 0.0000066
Prediction derivatives by MFK: [ y0 ]
0 : [ -62.1445 ]
1 : [ -54.2438 ]
2 : [ -45.0897 ]
3 : [ -35.1879 ]
4 : [ -25.1268 ]
5 : [ -15.5246 ]
6 : [ -6.96728 ]
7 : [ 0.0549673 ]
8 : [ 5.20445 ]
9 : [ 8.33791 ]
10 : [ 9.52639 ]
11 : [ 9.0485 ]
12 : [ 7.35596 ]
13 : [ 5.01416 ]
14 : [ 2.62452 ]
15 : [ 0.738605 ]
16 : [ -0.22404 ]
17 : [ -0.0420272 ]
18 : [ 1.26837 ]
19 : [ 3.44776 ]
20 : [ 6.02491 ]
21 : [ 8.38203 ]
22 : [ 9.84636 ]
23 : [ 9.79587 ]
24 : [ 7.76439 ]
25 : [ 3.53107 ]
26 : [ -2.81922 ]
27 : [ -10.8744 ]
28 : [ -19.917 ]
29 : [ -28.9875 ]
30 : [ -36.9827 ]
31 : [ -42.7774 ]
32 : [ -45.3526 ]
33 : [ -43.9181 ]
34 : [ -38.0104 ]
35 : [ -27.558 ]
36 : [ -12.9048 ]
37 : [ 5.20984 ]
38 : [ 25.7114 ]
39 : [ 47.2828 ]
40 : [ 68.4792 ]
41 : [ 87.8517 ]
42 : [ 104.067 ]
43 : [ 116.015 ]
44 : [ 122.885 ]
45 : [ 124.22 ]
46 : [ 119.935 ]
47 : [ 110.3 ]
48 : [ 95.9066 ]
49 : [ 77.5972 ]
___________________________________________________________________________
Evaluation
# eval points. : 50
Predicting ...
Predicting - done. Time (sec): 0.0003662
Prediction time/pt. (sec) : 0.0000073
<matplotlib.legend.Legend object at 0x7f1210b7ff40>
Total running time of the script: ( 0 minutes 0.193 seconds)
 otsmt
otsmt